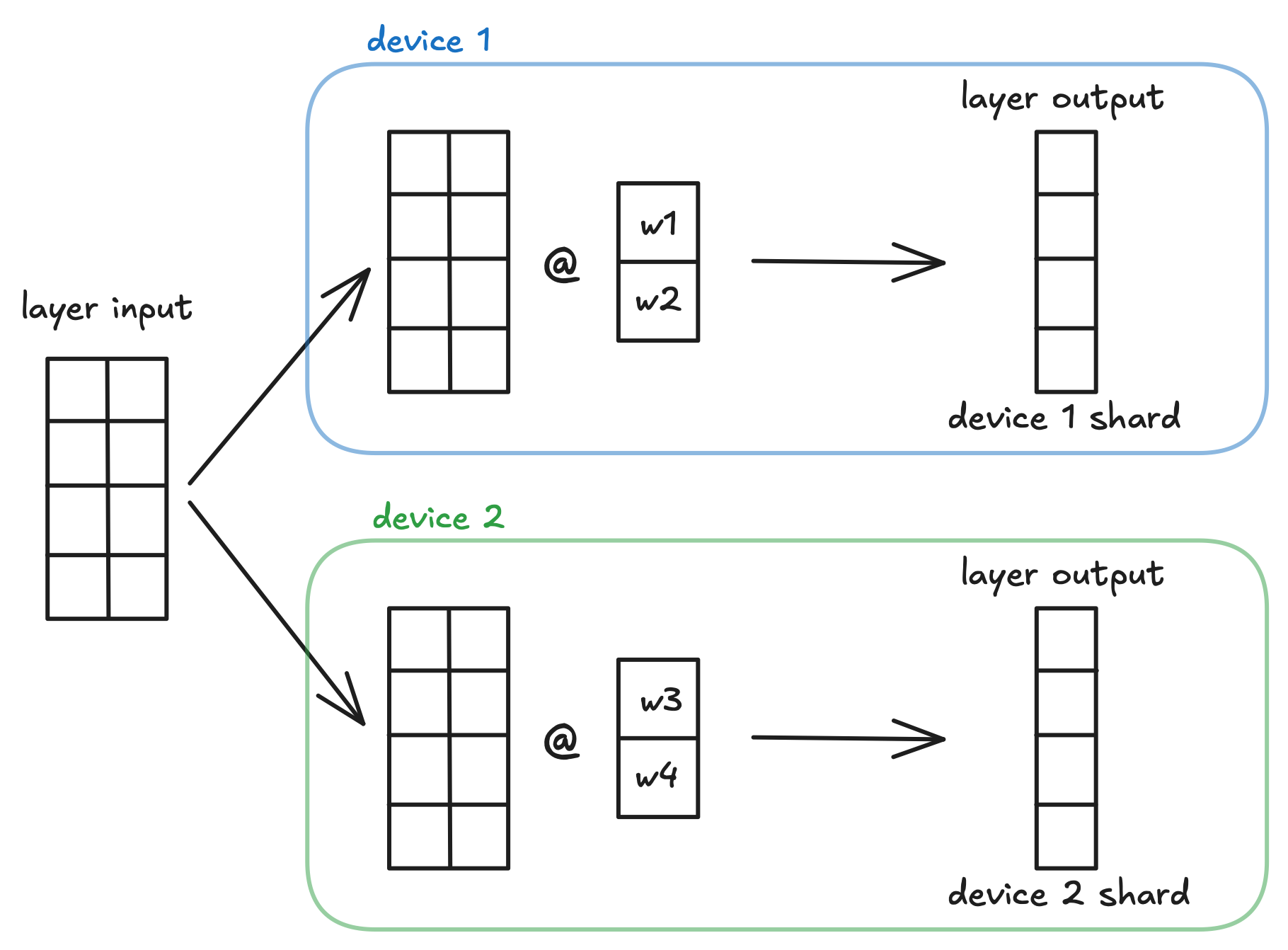
Tensor Parallelism

Tensor Parallelism#

In this example, we will explore how tensor parallelism (TP) works in MLX. We will start with an overview of the distributed layers in mlx.nn and then show how to do tensor parallelism Llama-style transformer models.

Sharded Layers#

AllToShardedLinear#

This layer replicates a common input and shards the weight matrix along the output dimension across all devices in the mlx.core.distributed.Group. The layer produces a sharded output.

For example, consider an mlx.nn.AllToShardedLinear layer with input_dims=2 and output_dims=2, a batched input of shape (4, 2), and a device group with 2 devices. The layer shards the weight matrix along the output dimension across the two devices, where each device receives the full input and computes a partial output.

column-wise tensor parallelism

This layer does not automatically gather all outputs from each device. This is an intended and useful design choice.

QuantizedAllToShardedLinear is the quantized equivalent of mlx.nn.AllToShardedLinear. Similar to mlx.nn.QuantizedLinear, its parameters are frozen and will not be included in any gradient computation.

ShardedToAllLinear#

This layer expects inputs that are sharded along the feature dimension and shards the weight matrix along the input dimension across all devices in the mlx.core.distributed.Group. The layer automatically aggregates the results using mlx.core.distributed.all_sum, so all devices in the group will have the same result.

For example, consider an mlx.nn.ShardedToAllLinear layer with input_dims=2 and output_dims=2, a batched input of shape (4, 2), and a device group with 2 devices. The layer shards the weight matrix along the input dimension across the two devices. Each device computes a (4,2) output, which is then aggregated with all other device outputs to get layer output.

row-wise tensor parallelism

This layer does not automatically shard the inputs along the feature dimension for you. It is necessary to create a “partial” input structure to feed into the layer. This is an intended and useful design choice.

QuantizedShardedToAllLinear is the quantized equivalent of mlx.nn.ShardedToAllLinear. Similar to mlx.nn.QuantizedLinear, its parameters are frozen and will not be included in any gradient computation.

Shard Utility Functions#

shard_linear#

Converts a regular linear layer into a tensor parallel layer that distributes computation across multiple devices. Takes an existing mlx.nn.Linear or mlx.nn.QuantizedLinear layer and returns a new distributed layer (either mlx.nn.AllToShardedLinear or mlx.nn.ShardedToAllLinear, depending on the sharding type). The original layer is not modified.

shard_inplace#

Splits the parameters of an existing layer across multiple devices by modifying the layer in-place. Unlike shard_linear, this function does not create a new layer or add distributed communication. The layer itself must handle distributed communication if needed.

Useful Design Choices#

The design choices above regarding when operations are done automatically are intentional and make model training and inference easier.

All-to-sharded and sharded-to-all layers naturally go together because the output of the former layer is exactly the input needed needed for the latter. This removes the need for an intermediate gather step between the layers, reducing communication overhead.

This is why mlx.nn.AllToShardedLinear does not aggregate results automatically and why mlx.nn.ShardedToAllLinear does not shard inputs automatically. It is so that they can be placed in successive order and work together easily.

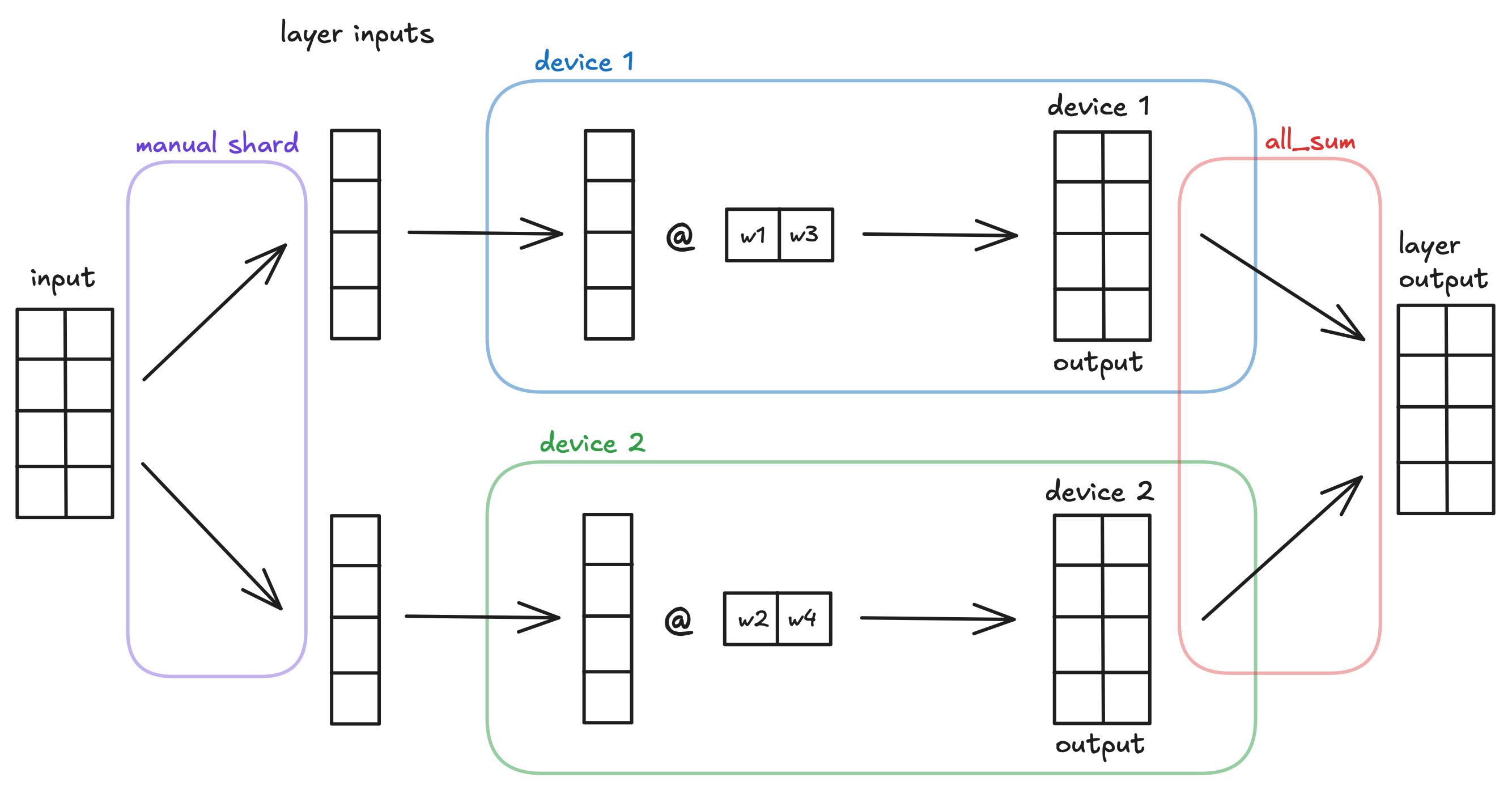
We can demonstrate this through a simple model using our two types of distributed layers.

x = ... # some (4, 2) model input: batch size 4, feature size 2

l1 = nn.AllToShardedLinear(2, 2, bias=False)   # initialize the layer
l1_out = l1(x) # (4, 1) output

l2 = nn.ShardedToAllLinear(2, 2, bias=False)
l2_out = l2(l1_out) # (4, 2) output
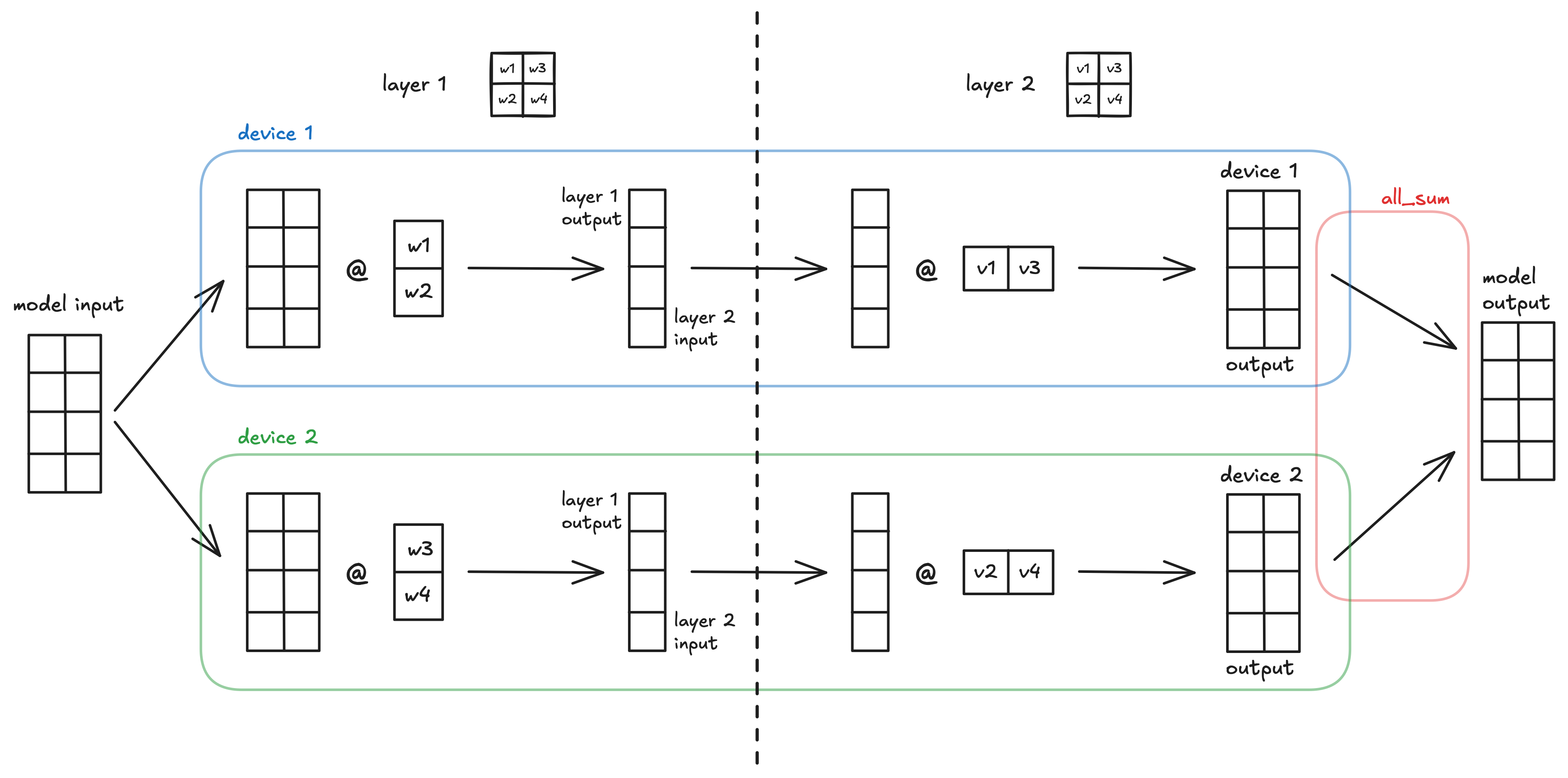
two layer tensor parallelism

A visualization of the simple MLX model using all-to-sharded then sharded-to-all tensor parallelism across 2 devices.

LLM Inference with Tensor Parallelism#

We can apply these TP techniques to LLMs in order to enable inference for much larger models by sharding parameters from huge layers across multiple devices.

To demonstrate this, let’s apply TP to the Transformer block of our Llama Inference example. In this example, we will use the same inference script as the Llama Inference example, which can be found in mlx-examples.

Our first edit is to initialize the distributed communication group and get the current process rank:

world = mx.distributed.init()
rank = world.rank()

Next, let’s look at the current architecture of the transformer block and see how we can apply tensor parallelism:

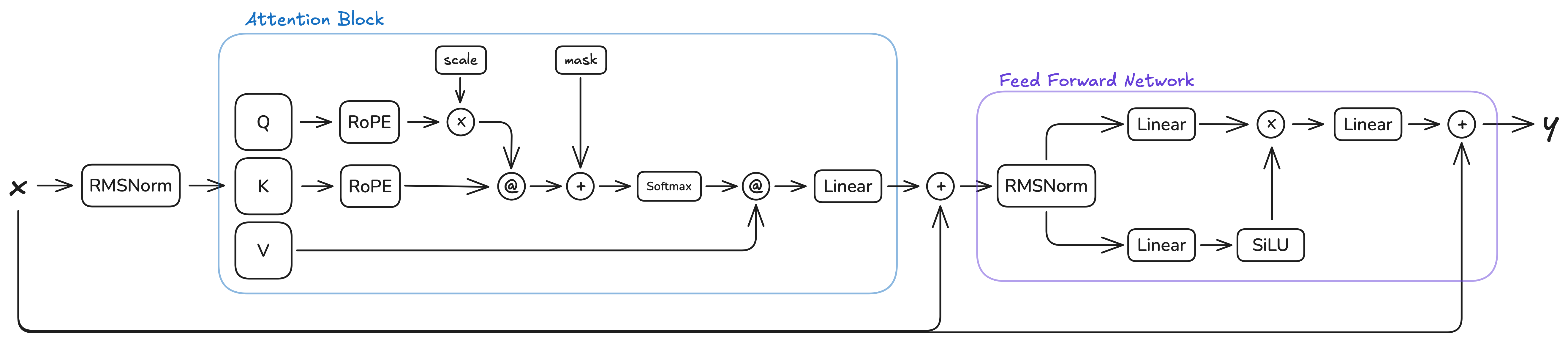
llama transformer example

This architecture has two natural places where tensor parallelism can be applied: the attention block and the FFN block. Both follow the same pattern: multiple parallel linear layers operating on the same input, followed by a single output linear layer. In the attention block, the Q, K, and V projections are sharded along the output dimension (all-to-sharded), and the output projection is sharded along the input dimension (sharded-to-all). Similarly in the FFN block, the gate and up projections become all-to-sharded layers, and the down projection becomes an sharded-to-all layer.

The intermediate operations between the linear layers (RoPE, softmax, scaled dot-product attention in the attention block, and element-wise multiplication in the FFN block) do not impede the use of our TP paradigm. These operations are either:

  • Element-wise operations (RoPE, element-wise multiplication): These operate independently on each element or position, preserving the sharding pattern without requiring cross-device communication.

  • Operations on non-sharded dimensions (softmax, scaled dot-product attention): These operate along dimensions that are not sharded (such as the sequence length or head dimensions), so they can be computed independently on each device. The attention computation Q @ K^T and scores @ V work correctly with sharded Q, K, V tensors because the matrix multiplications are performed along the sharded feature dimension, and the results remain properly sharded for the subsequent sharded-to-all layer.

To implement sharding in our Llama inference, we use shard_linear to get sharded linear layers with distributed communication. This is easier than using shard_inplace and implementing the steps manually in the __call__ function.

The following code shows how to shard the Attention block. The Q, K, and V projection layers are converted to all-to-sharded layers, while the output projection is converted to a sharded-to-all layer. The number of heads are also adjusted to account for the sharding:

# ... in Attention class
def shard(self, group: mx.distributed.Group):
  self.n_heads = self.n_heads // group.size()
  self.n_kv_heads = self.n_kv_heads // group.size()

  self.wq = nn.layers.distributed.shard_linear(self.wq, "all-to-sharded", group=group)
  self.wk = nn.layers.distributed.shard_linear(self.wk, "all-to-sharded", group=group)
  self.wv = nn.layers.distributed.shard_linear(self.wv, "all-to-sharded", group=group)
  self.wo = nn.layers.distributed.shard_linear(self.wo, "sharded-to-all", group=group)

Similarly, the FeedForward block is sharded by converting the gate (w1) and up (w3) projections to all-to-sharded layers, and the down projection (w2) to a sharded-to-all layer:

# ... in FeedForward class
def shard(self, group: mx.distributed.Group):
  self.w1 = nn.layers.distributed.shard_linear(self.w1, "all-to-sharded", group=group)
  self.w2 = nn.layers.distributed.shard_linear(self.w2, "sharded-to-all", group=group)
  self.w3 = nn.layers.distributed.shard_linear(self.w3, "all-to-sharded", group=group)

Finally, in our load_model function, we need to apply our sharding functions to all transformer layers when using multiple devices:

# ... in load_model function
if world.size() > 1:
  # convert Linear layers in Transformer/FFN to appropriate Sharded Layers
  for layer in model.layers:
      layer.attention.shard(group=world)
      layer.feed_forward.shard(group=world)

This allows us to use the llama inference file as normal when running python llama.py, but now we can also run it across two (or more) devices via mlx.launch -n 2 llama.py.

Contents